Acest șir de numere, cunoscut și sub denumirea de „secvența Fibonacci”, este o secvență numerică în care fiecare termen este suma celor doi anteriori. Astfel, primele două valori ale șirului sunt 0 și 1, iar fiecare valoare ulterioară poate fi obținută prin adunarea celor două numere precedente. Secvența este extrem de simplă, dar impactul său asupra științei, naturii și culturii umane este profund și vast.
Originea și proprietățile șirului lui Fibonacci
Șirul lui Fibonacci își are originile în lucrarea matematicianului italian Leonardo Fibonacci, care a introdus această secvență în anul 1202 în lucrarea sa Liber Abaci. Deși Fibonacci a fost cel care a popularizat acest șir, secvența a fost deja cunoscută în diverse culturi antice, cum ar fi în India.
Cu toate acestea, Fibonacci a utilizat această secvență pentru a rezolva o problemă legată de creșterea populației de iepuri, problema fiind formulată astfel: „Câte perechi de iepuri vor exista într-un an, având în vedere că fiecare pereche produce o pereche de iepuri noi în fiecare lună, iar perechile de iepuri care ating vârsta de două luni pot începe să se reproducă?”
Secvența lui Fibonacci poate fi scrisă astfel:
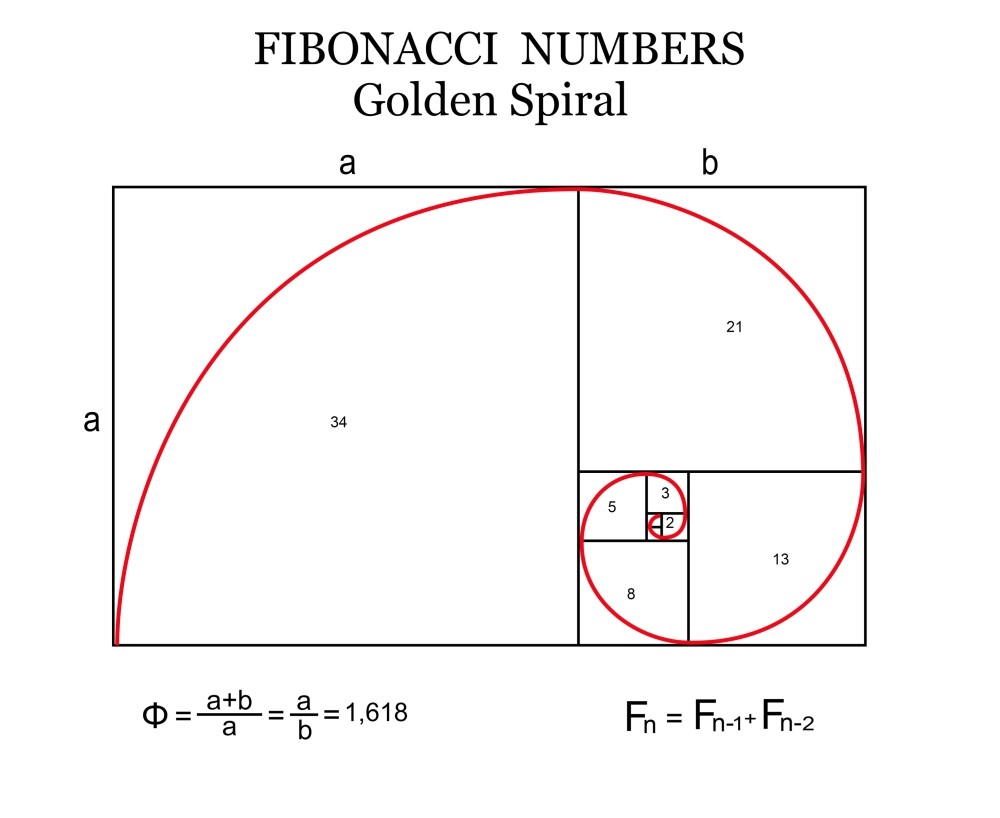
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…
Fiecare număr din această secvență este suma celor două numere anterioare. De exemplu, 5 + 8 = 13, 8 + 13 = 21 și așa mai departe. Deși pare o secvență simplă, ea are multe proprietăți interesante și aplicații în viața de zi cu zi.
Relația șirului lui Fibonacci cu natura
Unul dintre cele mai uimitoare aspecte ale șirului lui Fibonacci este prezența sa în natură. Pe măsură ce oamenii au început să studieze acest șir mai atent, au descoperit că multe structuri naturale se conformează unei proporții legate de secvența Fibonacci, oferind dovezi fascinante ale unei legături subtile între matematică și lumea naturală.
Un exemplu emblematic este numărul de petale ale florilor. Multe flori, inclusiv crizantemele și lalelele, au un număr de petale care corespunde unui număr din șirul lui Fibonacci. De exemplu, crizantemele pot avea 21, 34 sau chiar 55 de petale. Acest lucru poate fi explicat prin modul în care plantele cresc și se organizează, în special printr-un proces numit „fibonacci spiral” (spirală Fibonacci), care permite o creștere optimă și eficientă a plantelor.
Un alt exemplu este forma conurilor de pin și a conurilor de brad. Atunci când aceste conuri sunt privite de sus, se poate observa că spiralele formate pe suprafața lor urmează secvența lui Fibonacci. Aceste spirale se dezvoltă într-un mod care maximizează spațiul și asigură eficiența maximă în creșterea semințelor.
Relația cu secvența aurei și proporția de aur
Proporția de aur (denumită și „secvența aurei” sau „numărul de aur”) este o constantă matematică cu valoarea aproximativă de 1,618. Aceasta este legată direct de secvența lui Fibonacci. Dacă luăm două numere consecutive din secvența Fibonacci și împărțim numărul mai mare la numărul mai mic, rezultatul va tinde să se apropie de valoarea 1,618 pe măsură ce numerele cresc. De exemplu, 21 împărțit la 13 dă aproximativ 1,615, iar 144 împărțit la 89 dă aproximativ 1,618.
Proporția de aur a fost utilizată de-a lungul istoriei în arhitectură, artă și design pentru a crea structuri și compoziții vizuale armonioase. Multe dintre cele mai faimoase opere de artă, precum „Omul Vitruvian” de Leonardo da Vinci, sau chiar fațadele unor clădiri celebre, respectă această proporție. Ideea că forma și echilibrul natural pot fi descrise matematic prin șirul lui Fibonacci și proporția de aur a captat imaginația multor oameni, fiind o legătură între frumusețea naturală și ordinele matematice.
Fibonacci în matematică și tehnologie
Pe lângă aplicabilitatea sa în natură, șirul lui Fibonacci joacă un rol important și în matematică, algoritmică și informatică. De exemplu, șirul Fibonacci este folosit în dezvoltarea algoritmilor pentru căutarea și sortarea datelor. În special, algoritmul de căutare binară, care este esențial în majoritatea aplicațiilor software moderne, este bazat pe principiile secvenței Fibonacci.
De asemenea, în informatică, șirul Fibonacci este utilizat în analiza performanței algoritmilor și a problemelor de optimizare. Algoritmii de programare dinamică, care sunt folosiți pentru a rezolva probleme complexe și pentru a economisi timp și resurse, utilizează secvența Fibonacci pentru a reduce complexitatea problemelor.
Un alt domeniu în care șirul lui Fibonacci este important este criptografia. Anumite secvențe de numere, cum ar fi cele din șirul Fibonacci, pot fi folosite pentru a genera chei criptografice și pentru a securiza comunicațiile digitale.
O lume interconectată prin numere
Șirul lui Fibonacci este mult mai mult decât o simplă secvență matematică. Este un simbol al armoniei și al ordinii care reglează viața naturală și structura universului.
De la modul în care cresc plantele până la modurile în care oamenii își construiesc operele de artă și tehnologiile avansate, Fibonacci ne oferă o fereastră fascinantă către legile invizibile care guvernează lumea din jurul nostru.